JavaScript에서 조합(Combination) 구하기, 완전탐색 코드 상세 분석

조합은 수학에서 주어진 집합의 요소들을 선택하여 만들 수 있는 모든 경우의 수를 말합니다. 프로그래밍에서는 이러한 개념을 배열과 재귀 함수를 사용하여 구현할 수 있습니다. 여기서는 JavaScript를 사용하여 주어진 배열에서 n개의 요소를 선택하는 모든 조합을 구하는 코드를 분석해보겠습니다.
javscript 조합 살펴보기
함수 작동 방식
const getCombinations = function (arr, selectNumber) {
const results = []; // 조합의 결과를 저장할 배열
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = origin.slice(index + 1);
const combinations = getCombinations(rest, selectNumber - 1);
const attached = combinations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}
- 기본 조건 처리: selectNumber === 1일 때, 즉 조합으로 1개만 선택해야 할 때는 각 요소를 배열에 담아 반환합니다. 이는 재귀 호출의 기본 조건으로 작동합니다.
- 고정 요소(fixed)와 나머지 요소(rest)의 분리: 배열의 각 요소를 순회하며, 현재 요소를 고정(fixed)하고, 그 이후의 요소들을 나머지(rest)로 분리합니다. 이는 조합의 기준점을 설정하는 과정입니다.
- 재귀 호출을 통한 나머지 요소의 조합 구하기: 나머지 요소에 대해 재귀적으로 getCombinations 함수를 호출하여, 선택해야 하는 요소의 수(selectNumber - 1)에 대한 조합을 구합니다.
- 고정 요소와 나머지 요소의 조합(결합): 재귀 호출로부터 반환된 조합에 고정 요소를 붙여 새로운 조합을 만듭니다. 이 과정은 모든 가능한 조합을 만들어내는 핵심입니다.
- 결과 반환: 모든 조합이 저장된 results 배열을 반환합니다.
상세한 실행과정 설명
console.log(getCombinations([1,2,3,4],3)); 코드의 실행 과정을 상세하게 설명하겠습니다. 이 과정을 통해 조합 함수가 어떻게 재귀적으로 모든 가능한 조합을 찾아내는지 이해할 수 있습니다.
초기 호출

- getCombinations([1,2,3,4], 3) 함수가 처음 호출됩니다.
- selectNumber는 3입니다. 기본 조건인 selectNumber === 1에 도달하지 않았으므로, 조건문은 건너뜁니다.
첫 번째 재귀 과정
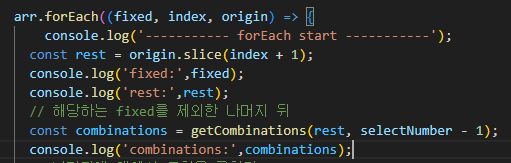
- forEach 반복문이 시작되고, 첫 번째 요소인 1을 고정(fixed)합니다.
- rest: [2,3,4]
- getCombinations([2,3,4], 2)가 호출됩니다.
두 번째 재귀 과정 (getCombinations([2,3,4], 2) 내부)

- 2를 고정하고, [3,4]를 나머지로 설정합니다.
- getCombinations([3,4], 1) 호출
- 여기서 selectNumber가 1이 되므로, [3], [4]가 반환됩니다.
- 반환된 배열 [3], [4]에 고정된 2를 추가하여, [2,3], [2,4]를 생성합니다.
첫 번째 재귀로 복귀

- 위에서 생성된 [2,3], [2,4]에 1을 추가하여, 최종적으로 [1,2,3], [1,2,4]가 만들어집니다.
- 같은 과정이 3과 4에 대해서도 반복되며, 각각 [1,3,4], [2,3,4] 조합이 추가로 생성됩니다.
전체 과정 요약
- 처음에 1을 고정하고 나머지 [2,3,4]에 대해 조합을 구합니다.
- 2를 고정하고 [3,4]에서 조합을 구해, [1,2,3]과 [1,2,4]를 얻습니다.
- 다음으로 2를 고정하고 나머지 [3,4]에 대해 조합을 구합니다.
- 여기서는 selectNumber가 3이므로 바로 재귀 호출에 들어가지 않고, 앞서 설명한 과정을 통해 [1,3,4] 조합이 추가됩니다.
- 마지막으로, [2,3,4] 자체가 하나의 조합으로 처리됩니다.
이렇게 재귀 함수를 사용하여 조합을 구하는 과정은 각 단계에서 고정된 요소를 기준으로 나머지 요소들의 조합을 재귀적으로 구하는 방식으로 진행됩니다. 이 과정을 통해, 주어진 배열에서 n개의 요소로 만들 수 있는 모든 조합을 효율적으로 찾아낼 수 있습니다.
이 코드의 핵심은 재귀 호출을 사용하여 조합의 가능성을 탐색하고, 각 단계에서 고정된 요소와 나머지 요소의 조합을 통해 최종 결과를 도출하는 것입니다. 이 방식을 통해 복잡한 조합의 문제도 단순화하여 해결할 수 있습니다.
▼30초 더 투자하면 얻게 되는 정보 ▼
JavaScript 배열 정렬 이해하기 sort((a, b) => a - b)의 원리,적용 방법
JavaScript 배열 정렬 이해하기 sort((a, b) => a - b)의 원리와 적용 방법 자바스크립트에서 배열의 요소를 정렬하는 일은 상당히 흔한 작업 중 하나입니다. 특히 숫자 배열을 오름차순 또는 내림차순으
lemonlog.tistory.com
코딩테스트 최소 힙(MinHeap)을 활용한 "더 맵게" 문제 해결법
코딩테스트 최소 힙(MinHeap)을 활용한 "더 맵게" 문제 해결법 프로그래밍 문제 해결에 있어 데이터 구조의 선택은 효율성을 결정짓는 중요한 요소입니다. "더 맵게" 문제는 스코빌 지수를 조작하
lemonlog.tistory.com
'Programming & Platform > JavaScript' 카테고리의 다른 글
| 자바스크립트의 역사, 웹 개발의 진화를 이끈 혁신의 여정 (1) | 2024.06.28 |
|---|---|
| 자바스크립트 프로토타입과 프로토타입 체인, 이해와 활용 (0) | 2024.06.25 |
| JavaScript 배열 정렬 이해하기 sort((a, b) => a - b)의 원리,적용 방법 (1) | 2024.03.18 |
| 3분 만에 배우는 자바스크립트 객체 지향 프로그래밍, 기초부터 실전까지 (0) | 2024.03.12 |
| 자바스크립트 프로토타입으로 배우는 객체 생성과 상속의 모든 것 (0) | 2024.03.12 |



